To strive, to seek, to find, and not to yield
Erik Boss
2016-09-22
1 Who is this guy?
- Erik Boss
- Ruhr-Universität Bochum
- Embedded Security Group (EMSEC)
- ECRYPT-NET ESR
1.1 What is he doing here?
- Large-scale (exhaustive) search problems
- For crypto
- Approach
- Problems, solutions and observations
2 The Use Case
Finding S-Boxes with Efficient Masking in Hardware
2.1 Why?

2.1.1 But also…
- Physical/implementation attacks
- Countermeasures
- S-Boxes
- Inherently maskable
- By construction
- Efficient and secure
2.1.2 But for this presentation…
Whole Lotta Searchin' Goin' On
3 Limiting Scope

3.1 S-Boxes
"That thing that AES uses."
- Intuition: n-bit to n-bit lookup tables
- n=8
- Common in symmetric ciphers
- Non-linear
3.2 Feistel Networks
"That thing that DES has."
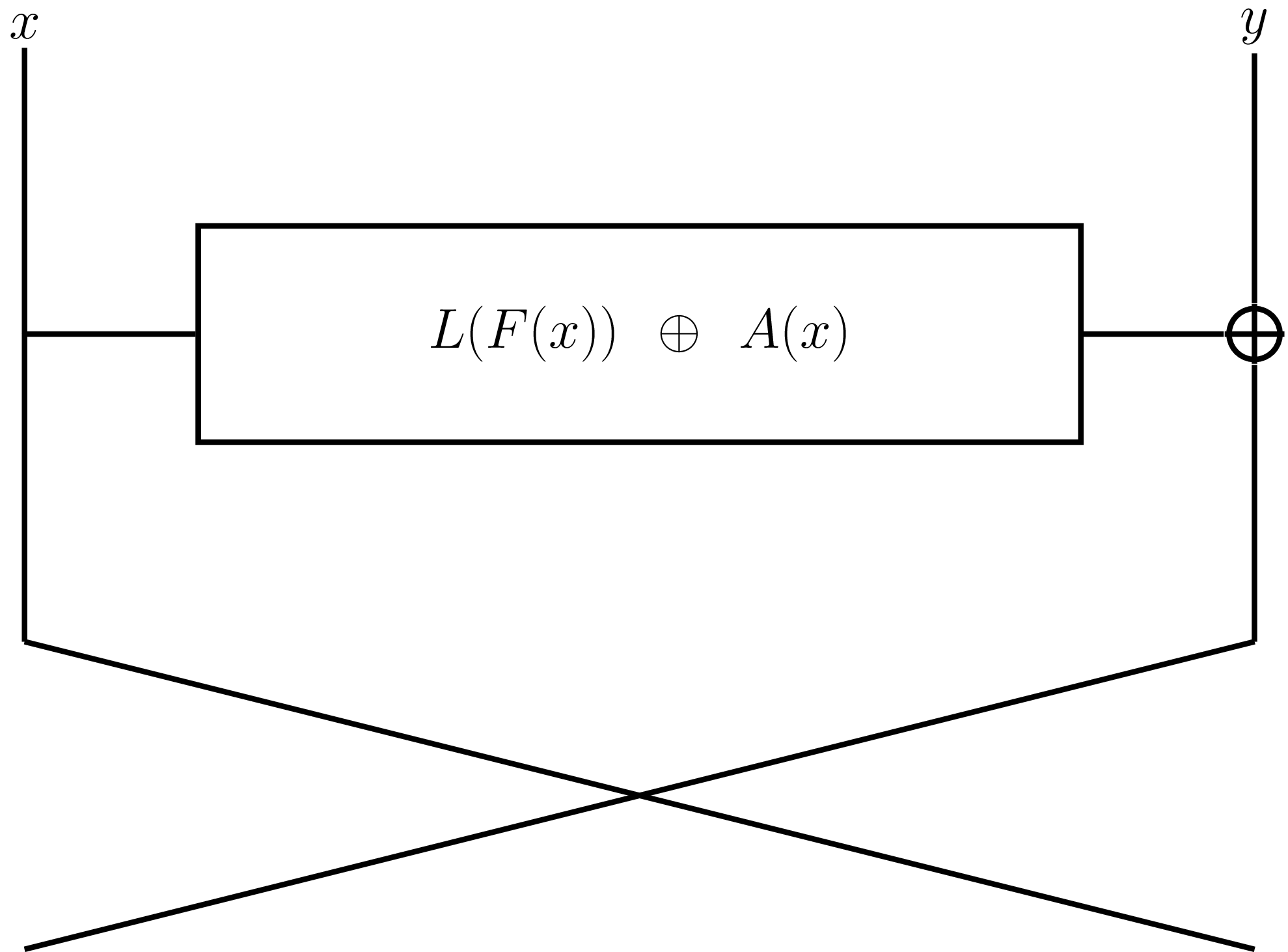
4 Recon

- Round function is a 4-bit to 4-bit function.
- \(2^{64}\) candidates

\(H(x) = L(F(x)) \oplus A(x)\)
- \(L(x)\): linear function
- \(A(x)\): affine function
- \(F(x)\): function corresp. to 4713 equivalence classes
\(2^{16} \cdot 2^{20} \cdot 4713 \approx 2^{48}\)
But we can reduce to \(\approx 2^{46.5}\)
Minimize search space.
– First rule of Find Club
Minimize redundancy.
– Third rule of Find Club
5 Secure?
"What's in the box!?"
- Algebraic Degree
- AES: 7
- Linearity, \(\le 64\)
- AES: 32
- Differential Uniformity, \(\le 16\)
- AES: 4
6 Approach
"Good luck storming the castle."
- Iterate over all L, A, F.
- Embarrassingly parallel
- Filter
- On?
6.1 Parallelism
"Power! Unlimited power!"
- GPUs to the rescue
- CUDA/OpenCL
Per thread/work item/core/…:
- Compute S-Box \(S\) for \(L\), \(F\), \(A\) corresp. to thread
- Compute a diff(\(S\)) check (\(\le\) threshold)
- Compute auxiliary properties
- Output those results that meet all criteria
7 Optimization
"The root of all evil."
Let's talk about rule #3 again.
7.1 Precomputation
- \(L\) & \(A\) are fairly small.
- A metric !@#$-ton of memory on our GPUs.
- Precompute tables for \(L\) & \(A\)
- Better: \(L \circ F\) and \(A\) for fixed \(F\)
- (Even better: store in cached memory)
Precompute, precompute, precompute.
– Fourth rule of Find Club
7.2 Breaking the Rules
Kids, don't try this at home.
Idea:
- Merge computation and filter(s)
- Terminate early
- Instruction divergence
Better: but within the same parallel context.
7.3 Differential Uniformity
sbox = [...] maximum = 0 for alpha in range(1, 256): hist = [0] * 256 for x in range(0, 256): beta = sbox[x] ^ sbox[x ^ alpha] hist[beta]++ maximum = max(maximum, hist[beta])
- Terminate after `maximum` reaches threshold
- Remove redundancy by:
- \(S(x) \oplus S(x \oplus 128) = S(x \oplus 128) \oplus S((x \oplus 128) \oplus 128)\)
- Merge by interleaving filter and S-box computation
- Observation: most iterations terminate after \(\alpha = 128\)
Terminate early, in concert.
– Fifth rule of Find Club
8 Addendum
Optimize for throughput.
– Sixth rule of Find Club
Mind the latency.
– Seventh rule of Find Club
9 Results
- Search time is approx. 2 weeks per iteration.
- For \(n \le 5\), a \(n\) iteration Feistel network with identical round functions will not give you better properties than:
- Degree 7, linearity 56, diff. uniformity 8, round function degree 2.
- Example of this class (selected for having a relatively low AND-gate complexity)
- F: 0001024704638EAD
- L: 028A9B1346CEDF57
- A: 6273627351405140
Welcome to Find Club. Enjoy your stay.